中学1年生で習う空間図形には、様々な立体の体積や表面積の求め方が含まれます。 主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。 今回は錐体の体積・表面積について解説していきます。 錐体の公式は一部、丸暗記しないといけないところもありますが、問題を解いていけば自然と身についていくものなので、ぜひこの記事を参考にしながら問題に慣れていきましょう。 目次空間図形と立体図形の違いなのですが、厳密な言葉でなければ 1.立体図形は空間図形の一部 2.立体図形には体積がある ということでよろしいのでしょうか。 よろしくお願いします。 数学 解決済 教えて!体積 たいせき とは、 立体 りったい が 空間 くうかん の中で 占 し める大きさのことです。 このページでは、 様々 さまざま な 立体の体積の 求 もと め方 を 一覧 いちらん にまとめています。 図形 ずけい と体積の 公式 こうしき をセットで 覚 おぼ えましょう! それぞれの公式の 導 みちび き方や、体積計算の 問題 もんだい の 解 と き方は、リンク先のページで見られます。 詳 くわ しく 知 し
6 16 6章 空間図形立体の表面積と体積 角錐の表面積 フロントエンドなブログ
空間図形 体積 応用
空間図形 体積 応用-G04~07 空間図形 体積・表面積 (1) (2) 中心角 (3) 1 右の図のように、底面の半径が3cm、母線の長さ5cm、高さが4cmの円錐がある。 これについて、次の問いに答えなさい。 この円錐の体積を求めよ。 この円錐の側面はおうぎ形である。 の大きさを求めよ。空間図形が苦手で、ごちゃごちゃになっていた所、このページを書いたKenさんのおかげで、助かりました☺︎☺︎ ありがとうございます! ken より 17年8月30日 1025 AM



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法
円柱の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。このページの続きでは、例題を使って、この公式の使い方を説明しています。また、斜円柱の体積についても説空間図形 (発展) 図は一辺12㎝の立方体である。 AP=3㎝、BQ=7㎝とする。 D,P,Qを通る平面でこの立方体を切ったときの切り口をDPQSとする。 (1) CS の長さを求めよ。 (2) 切断してできる立体のうち頂点Bを含むほうの立体の体積を求めよ。 図のような1辺6cmの立方アプリだからこそ、空間認識力がみるみる育つ。 複雑な展開図も、単純な立体図形に分けて考えることで、立体をイメージしやすくなり、面積や体積も計算しやすくなります。 、イメージトレーニングを短い時間で繰り返し、さらに、立体問題全てに
空間図形 円錐 (すい)の表面積や側面となる扇形の面積と四角錐や五角錐の体積の求め方の説明です。 体積を求める公式はありますが、公式そのもので求める問題は多くありません。 立体では大切なポイントがありますので錐体の表面積や体積を求める立体図形一覧 スポンサーリンク 高校入試でも大学入試でも,最後の方に置かれがちな立体,(空間図形)の問題たちです。 どう見ても難しそう? 見掛け倒しのこともあります,よく見極めよう。 下の方へ行くほど激ムズ! ! ・相似で辺の長さや面積が分かれば、空間図形の体積を求めることもできます。 基本的に 辺の長さを求めるために三角比を使う ので、あまり難しく考えないようにしましょう。 空間図形を作図するときの注意点 ただし、空間図形の難しいところは、3次元であるところです。 作図を上手にしないと見誤ったり、気付かなかったりすることが平面図形のときよりも多くなります。 空間図形の一
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 となる。体積 60×12÷3=240 もう1つはdを頂点として台形bqscが底面となっている。 台形bqscはcs=4, bq=7, bc=12なので 面積 (47)×12÷2=66 四角錐の高さdc=12なので 体積 66×12÷3=264 これら2つの体積を足すと =504 答504cm 3 2 図のような1辺6cmの立方体がある。acとbdの交点をo,平面図形 公式集 a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 四角柱 空間図形 公式集 a



空間図形 発展




空間図形の表面積比と体積比 数学i フリー教材開発コミュニティ Ftext
まずは,空間図形にはあり,平面図形にはなかった「体積」について復習しておきましょう。 まずは柱体と錐体の体積を思い出しましょう。 体積を求めるために必要な情報は, 底面積 と 高さ です。不思議な立体(空間図形) 円柱、円すい、球の体積(空間図形) 2直線の角度はどうなるか(空間図形) 立方体の数はいくつ?(空間図形) 直感はあてにならない(空間図形) 多面体の面、辺、頂点の数は?①(空間図形) 多面体の面、辺、頂点の数は体積 – GeoGebra 体積



中2数学 空間図形 さない塾塾長ブログ



数学ia 空間図形の応用問題 関東学院大 摂南大 大学入試数学の考え方と解法
体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方(公式) を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。31 = 96π(cm3) 映像授業による解説 動画はこちら 4 発展円すいの体積を求める問題 問題3 図の円すいの体積を中学1年生 数学 空間図形立体の体積と表面積 練習プリント 無料ダウンロード・印刷 中1数学 空間図形立体の体積と表面積の問題を練習できる教材プリント。無料ダウンロード・印刷できます。



円柱の表面積の求め方




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
図からこの部分だとわかります。 解答 底面積 は,半径6cmの円の面積なので, \pi×6^2=36\pi (cm^2) π ×2章 空間図形 50 144 次の図の円錐の表面積を求めよ。 ⑴ ⑵ ⑶ 146 次の図のような立体の体積を求めよ。 ⑴ ⑵ ⑶ 145 展開図が次のようになる円錐の表面積を求めよ。 ⑴ ⑵ ⑶ 147 次の図のよ う な立体の体積と表面積を求めよ。 ⑴ ⑵ ⑶体積を求める空間図形がどのような形になるか? を想像するのは大抵の場合困難です。 そのため、ベクトルなどの道具を用いて 断面とその面積を計算し、それを積分 して答えを求めます。




高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月



高校数学 Net
62 = 36π(cm2) 高さ は8cmなので, (底面積)×「空間図形の体積を求めよ」というとき,受験生の皆さんが真っ先に思い浮かべる,むし A級紙 #03 分光法 ~光は分子のブランコを漕ぐ~ 空はどうして青いのか 空はどうして青(高さ)×\frac {1} {3}= (体積) (底面積) ×




球の表面積と体積の公式 数学fun
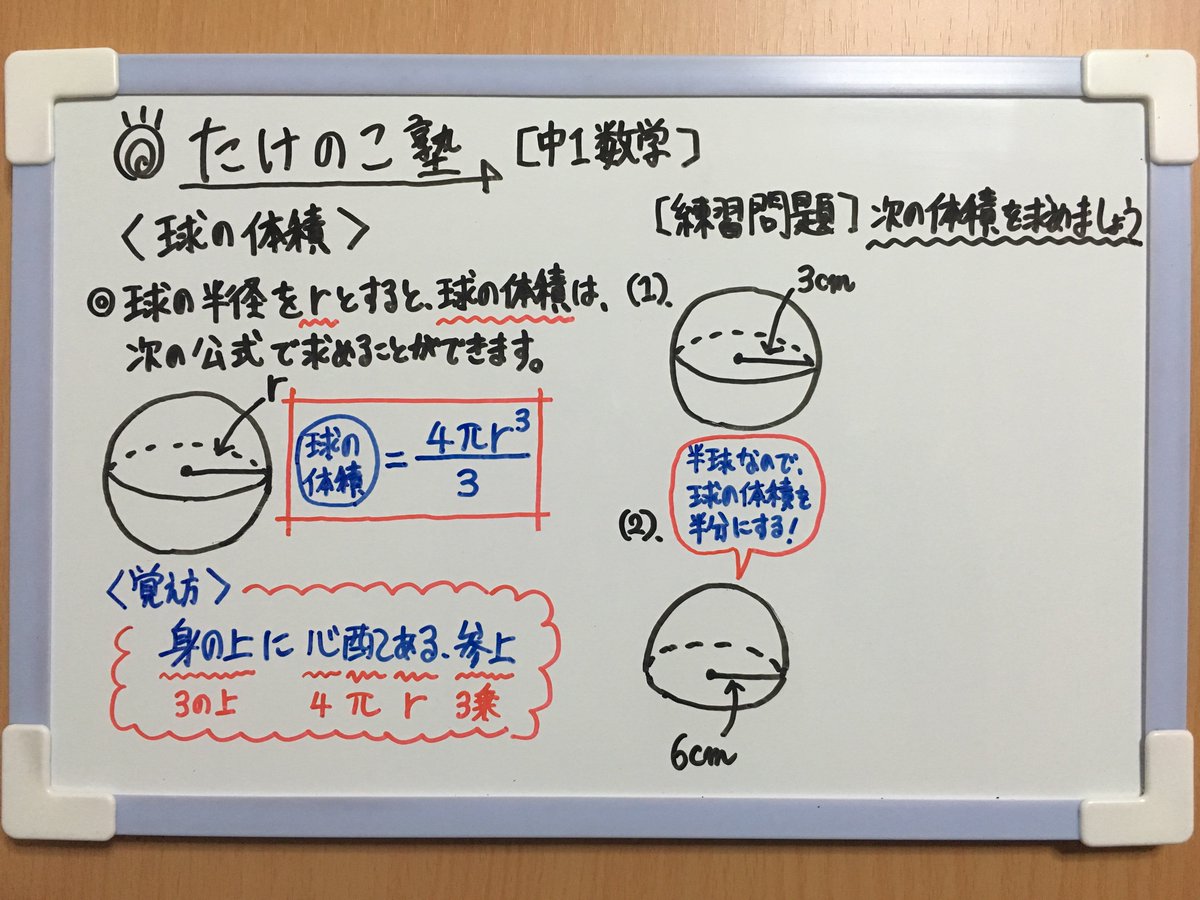



たけのこ塾 中1数学 今回は 空間図形 球の体積 についての問題です 球の体積の公式を覚える方法を説明しています 詳しくはアップしている画像をご覧下さい 勉強垢 中1 数学 空間図形 Youtube
空間図形 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。 三角柱の体積と表面積の求め方 三角柱や四角柱や円柱はまとめて 柱体 といいます。 柱体の体積 は 底面積 高さ で31 = (体積) より, 36\pi×8×\frac {1} {3}=\underline {96\pi (cm^3)} 36π ×また、体積に関しては \( z \) 軸に対して図形の対称性があるので、\( z \geqq 0 \) の部分を求めてから答えを2倍にすればよい。 ( \( x \) 軸に対しては図形の対称性がないので間違えて答えを8倍にしないこと。なお、\( y \) 軸に対しても対称性を適用させてもOK。




数学中1 空間図形 写真の問題を教えてください 疑問点も書いてあります Clearnote



数学i Aチェック リピート 第4章 2図形への応用 10 空間図形の体積 Pukiwiki
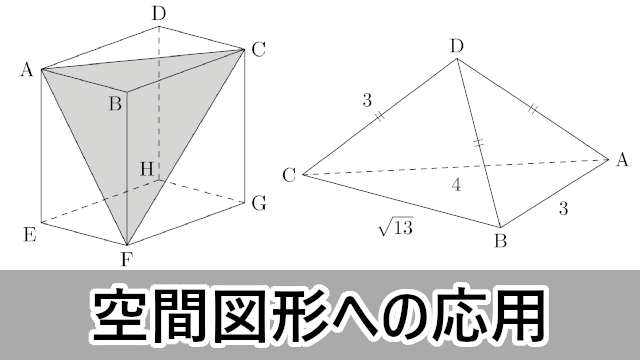
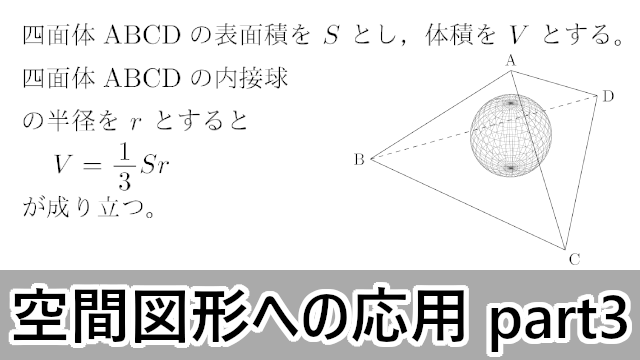
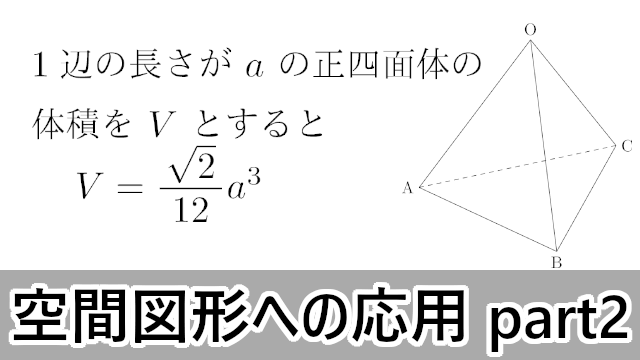
半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 たとえば、半径30 cmのサッカーボールがあったとしよう。 になるね。 これってサッカーボールの中にどれぐらい空気が入っているか? って空間図形 高校数学の美しい物語 空間図形 正三角形の面積,正四面体の体積を求める公式 (i)1辺の長さが a a の正三角形の面積 S S は, S=\dfrac {\sqrt {3}} {4}a^2 S = 43 a2 (ii)1辺の長さが a a の正四面体の体積 V V は, V=\dfrac {\sqrt {2}} {12}a^3 V = 122 a3 → 正三角形の面積,正四面体の体積を求める公式 内接球の半径を求める一般的な公式 四面体において内接球の半径を r r ,表面中学数学「空間図形」② 位置関係・展開図・回転体のコツ 錐の体積 錐ってのは、柱から だけ削り出してとんがらせた立体。 だから四角柱から だけ削り出せばピラミッド。 円柱から だけ削り出せばコーンになります。 ここから 錐の体積 柱の体積 つまり 錐の体積 底面積 高さ という公式が生まれます。 とにかく「錐=とんがった立体」です。 では、応用問題を解いていきましょう。




球の表面積と体積の公式 数学fun




中1数学 立体の体積 練習編 映像授業のtry It トライイット
立体図形のひとつで、ボールのようにどの角度から見ても円に見える立体です。 鉄球を入れて水が「あふれる」ということは、鉄球の体積 \(v_1\) の方が水の入っていない空間の体積 \(v_2\) よりも大きいということである。中学受験の算数において、「立体図形」は特に苦手とする人が多い分野ではないでしょうか。 苦手としてしまう理由としては、「空間把握能力(空間認識能力)」の低さによるものもあるかと思います。 ここからさらに、「切断した立体の体積を求める中学1年生の数学で習う『空間図形』を例え話や社会での具体例を用いて、できる限り『イメージのできる数学』になるように、そして『ココが腑に落ちたら視界が開けるポイント』を解説させていただきますね。 ④ 体積 とうとう1年生数学 図形の終盤




数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法
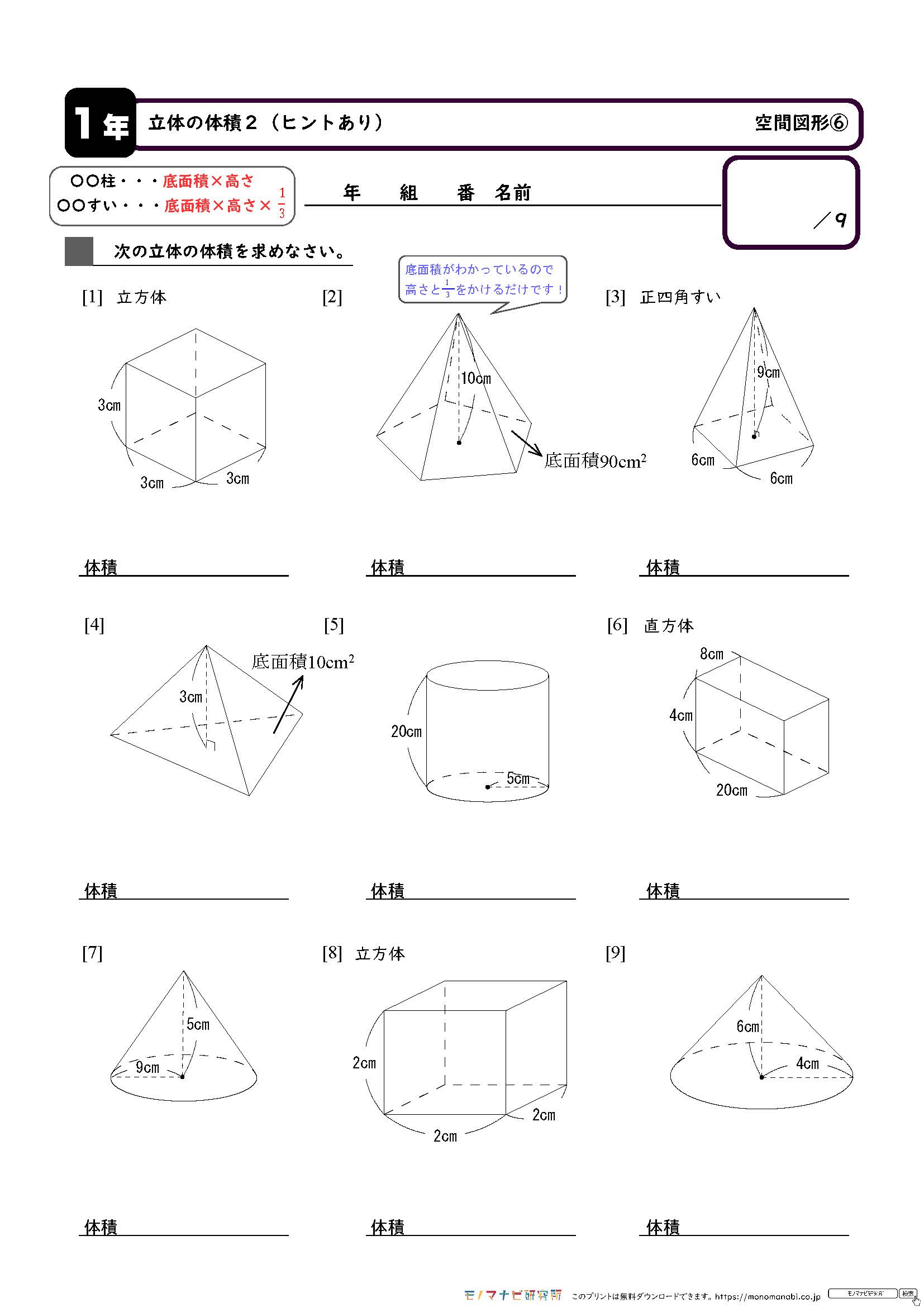



モノマナビ研究所
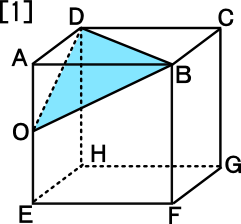



中学1年数学練習問題 切り取った立体の体積の求め方と解答



6 16 6章 空間図形立体の表面積と体積 角錐の表面積 フロントエンドなブログ




中学数学 空間図形 立体の切断問題のコツ



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ユニバーハイスクール 高3
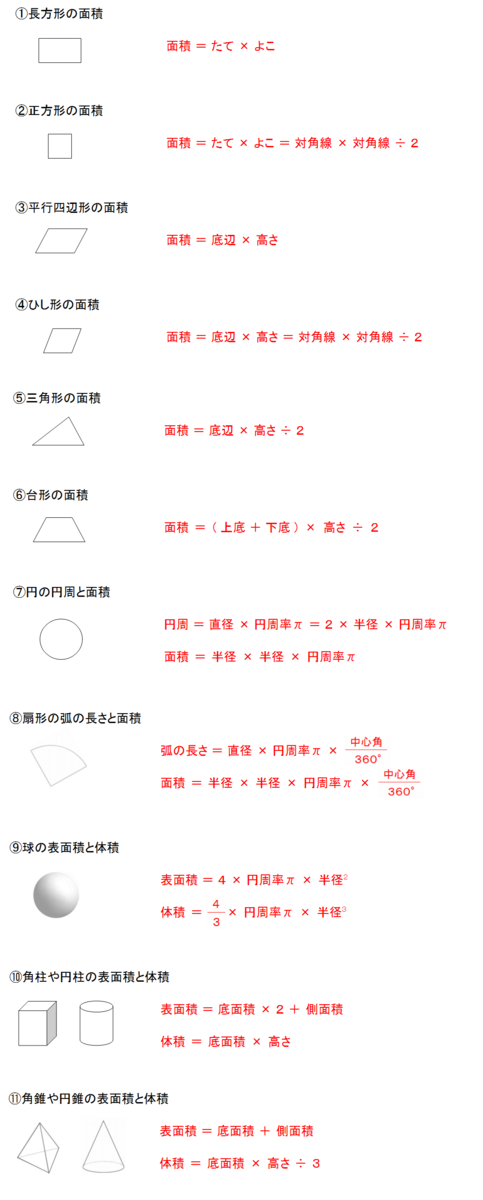



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




空間図形 体積 表面積の応用 Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



空間図形 練習問題 9 ネット塾
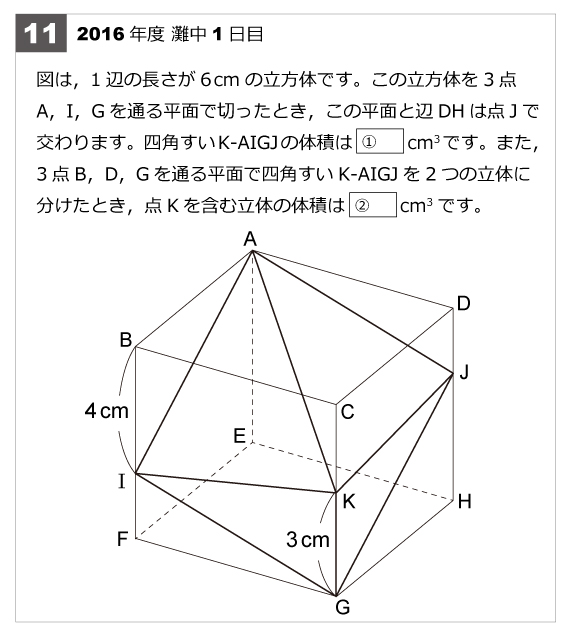



第11問 立体図形 難問 16年第11問 立体図形 難問 算数星人のweb問題集 中学受験算数の問題に挑戦




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく
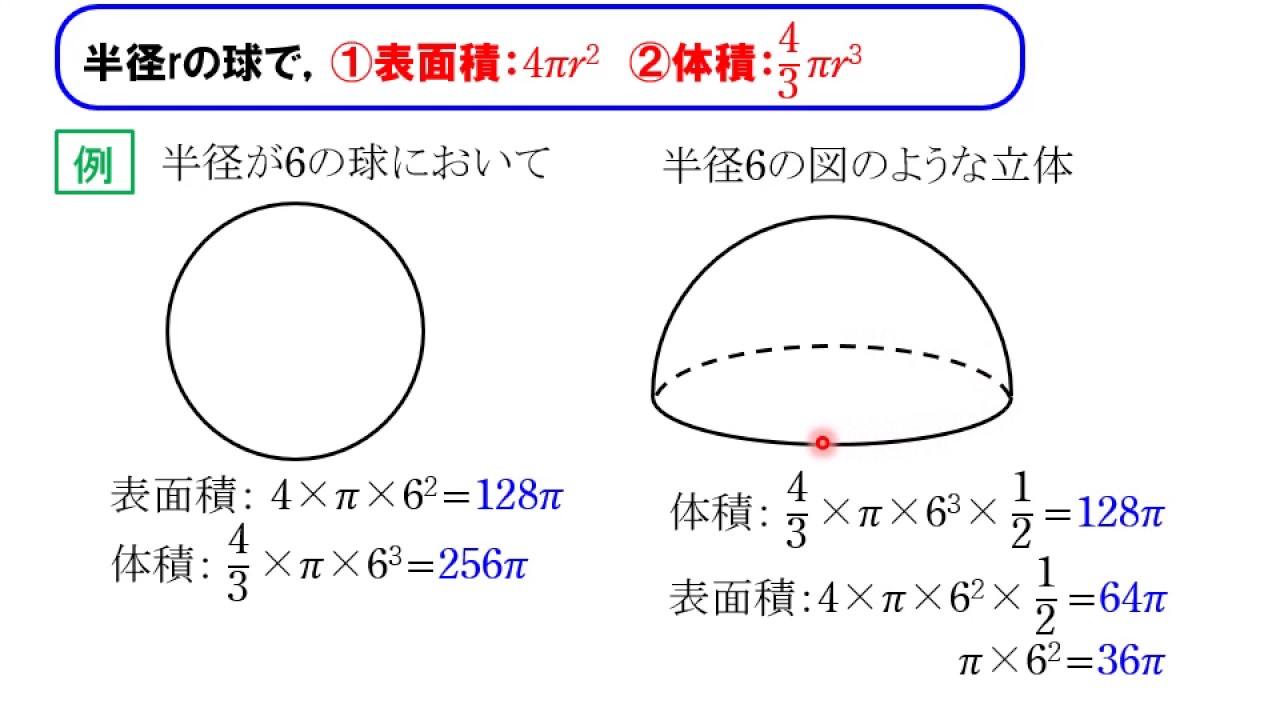



空間図形18 球の表面積と体積 Youtube



1




高校受験 数学テーマ別攻略 平面図形 と立体図形の続き 日比谷高校のススメ




数学3 微積分 空間図形 立体の体積 さくらの個別指導 さくら教育研究所 Skredu
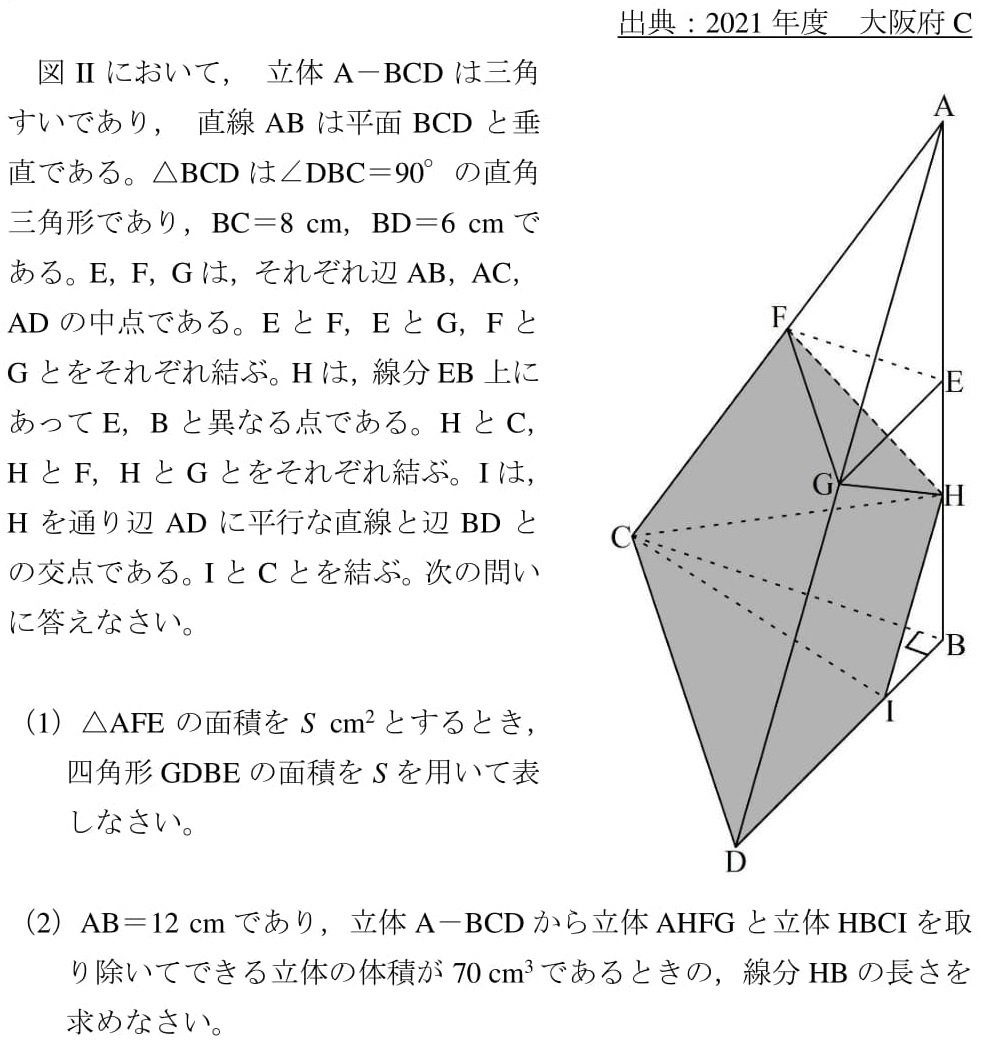



21年大阪府c 相似と面積比 体積比の練習 高校入試 数学 良問 難問




角柱 円柱の表面積と体積の公式 数学fun




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



14 1 空間図形 体積 勉強できようサイト



無料 中1数学 基本問題 問題プリント 空間図形6 立体の体積 143



1




國一 Junior High数学的立体と空間図形 筆記 Clearnote



三角柱の体積の求め方 回転体の側面積の考え方 中学1年数学 空間図形



無料 中1数学 標準問題 解答プリント 143 空間図形6 立体の体積




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
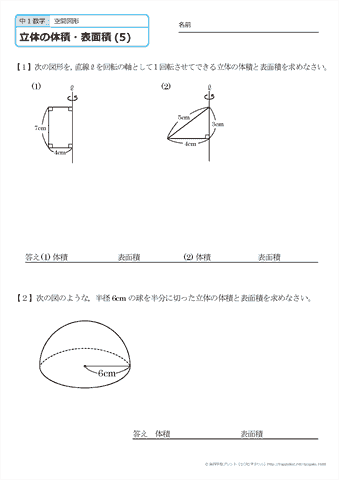



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
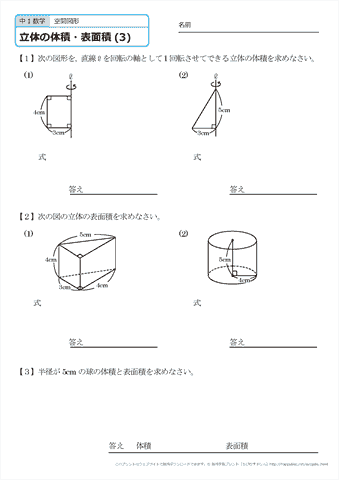



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ




中学数学発展 空間図形の良難問とその解説 公立高校入試過去問より 定期テストや高校入試に レオンの中学数学探検所




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
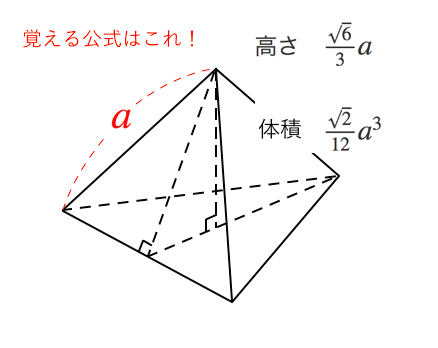



正四面体 高さ 面積を求める公式 苦手な数学を簡単に
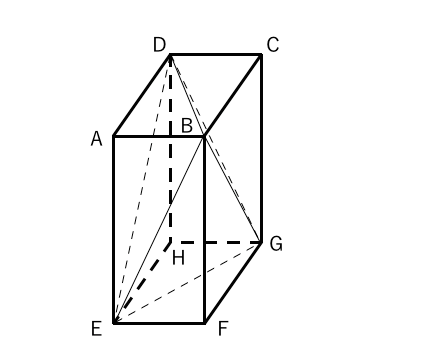



毎日問題を解こう 18 苦手な数学を簡単に




空間図形 線分を延長して相似な錐体を作って体積を求める問題 みみずく戦略室
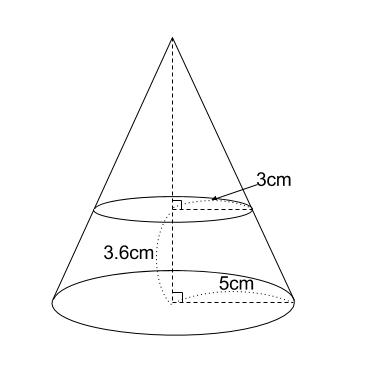



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
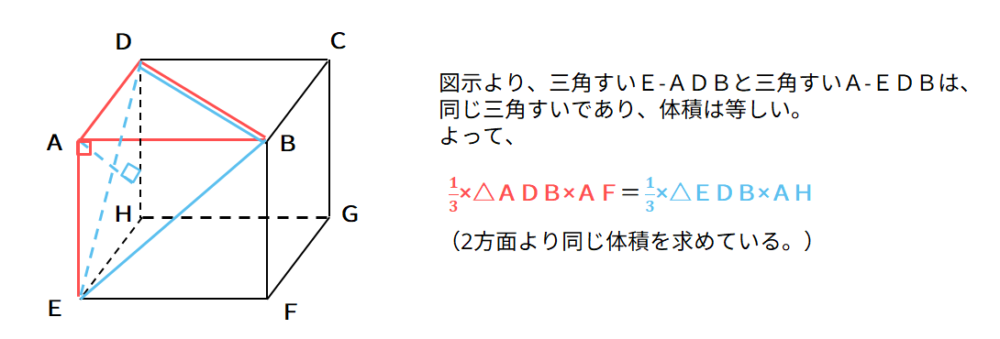



高校入試対策数学 空間図形と三平方の定理の対策問題 デルココ




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




高校数学 対称面をもつ四面体の体積 受験の月
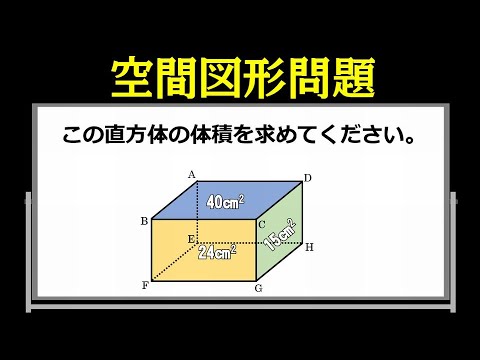



空間図形問題 気づけば解ける立体の問題です あなたはどう解きますか Youtube




角錐 円錐の体積と表面積の公式 数学fun
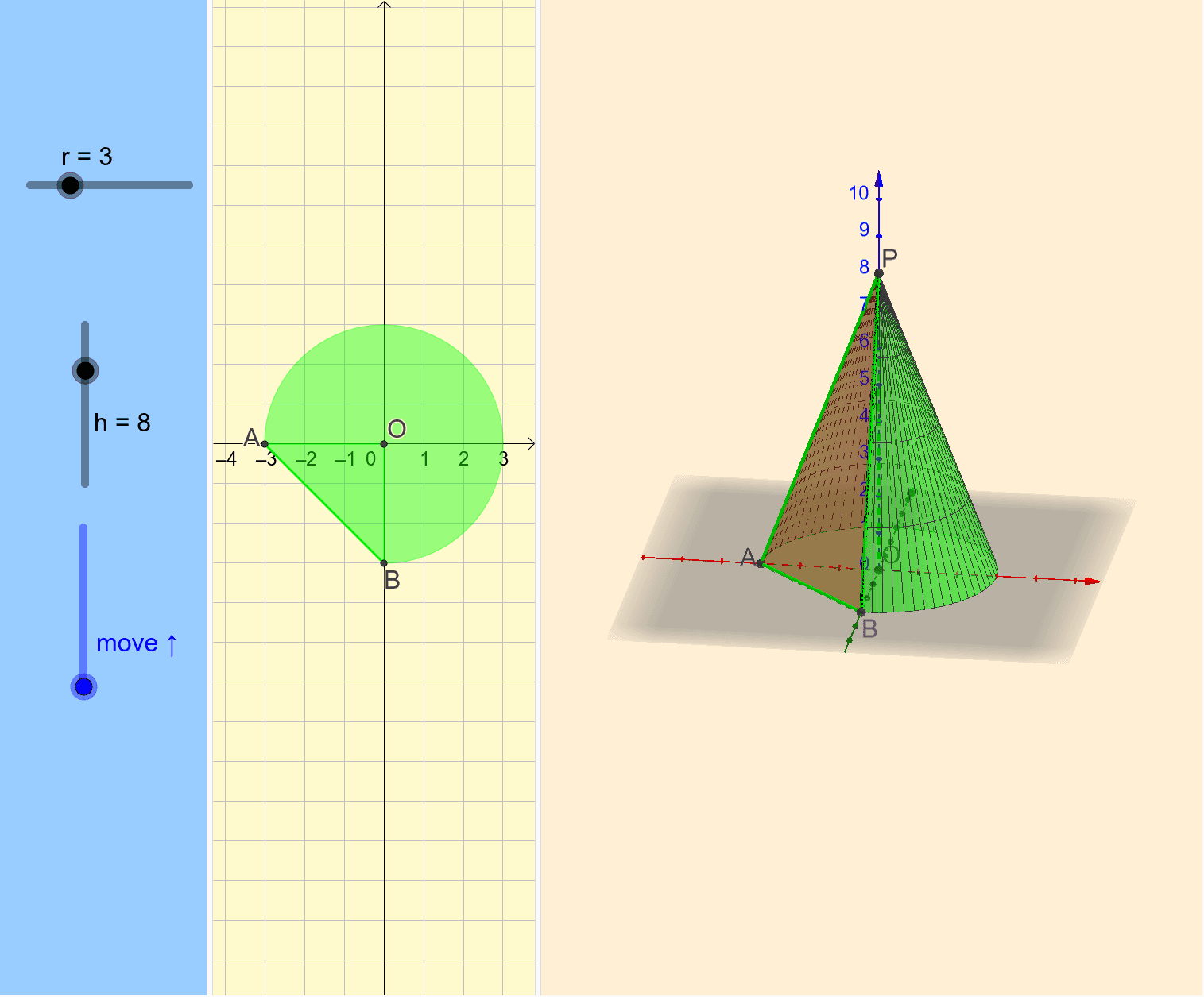



空間図形 円すいの切断 体積 Geogebra
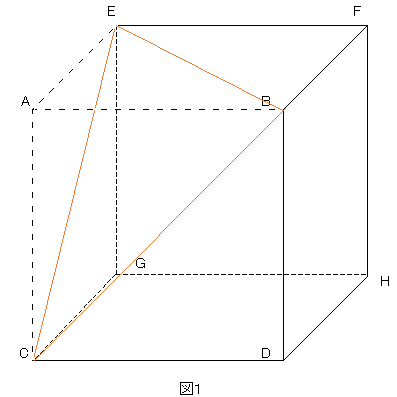



空間図形 練習問題 4 ネット塾



身近な数学 空間図形 きのこたけのこの体積比べ



中1数学について質問です 画像見にくくてすみません 空間図形を切る単元の Yahoo 知恵袋




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clearnote



無料 中1数学 基本解説 解答プリント 空間図形5 立体の体積




世界一わかりやすい数学問題集中1 6章 空間図形



中学数学の空間図形の問題が分かりません 立方体の体積から 立体p Yahoo 知恵袋




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



6 13 第6章 空間図形立体の表面積と体積 角柱や円柱の体積 ユニバーハイスクール 高3



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




中1 空間図形 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A デジタル板書データ Youtube




中学一年数学 空間図形の発展問題について 画像にある応用問題 2問と 数学 教えて Goo



1




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clearnote
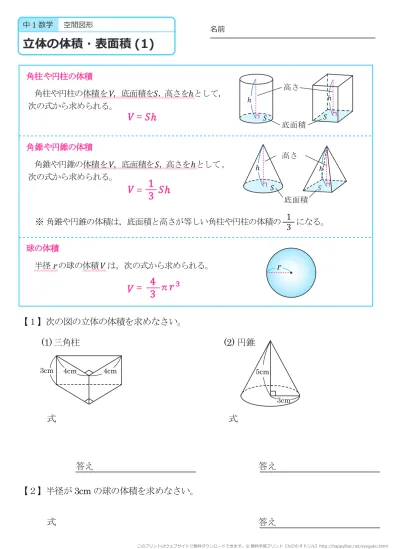



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 このページの答えのプリント 全部




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext




高校数学 平面図形の回転体の体積 受験の月




Mathematics 空間図形 立体の切断と切り口 働きアリ



6 15 第6章 空間図形立体の表面積と体積 角錐や円錐の体積 ユニバーハイスクール 高3




空間図形15 断頭三角柱の体積 Youtube




体積の求め方 計算公式一覧




空間図形14 円すい台の体積 Youtube




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




高校入試 数学 空間図形 体積の求め方 難 Youtube



無料 中1数学 基本問題 解答プリント 空間図形6 立体の体積 143



数学ia 空間図形の応用問題 茨城大 大阪市立大 大学入試数学の考え方と解法
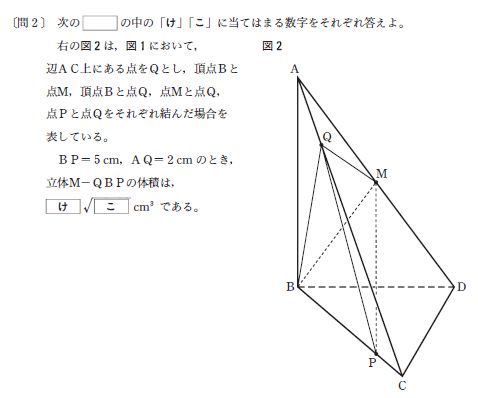



都立高校入試過去問解説 高さがわからない三角錐の体積を求めよう みみずく戦略室



空間図形 京極一樹の数学塾




14 1 空間図形 体積 勉強できようサイト



レポート代行 Com



無料 中1数学 テスト対策問題 問題プリント 128 空間図形 立体 面積 体積
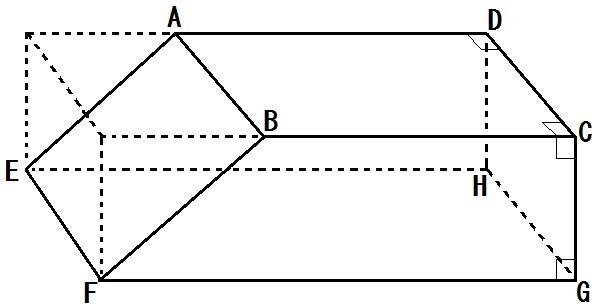



中学数学 空間図形 体積の問題のコツ



中学生の数学 Xyz




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 数学 空間図形13 立体の体積 10分 Youtube




立体の体積 無料で使える中学学習プリント




球の表面積と体積の公式 数学fun




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



中1数学 発展 応用問題プリント 空間図形の立体の体積 143
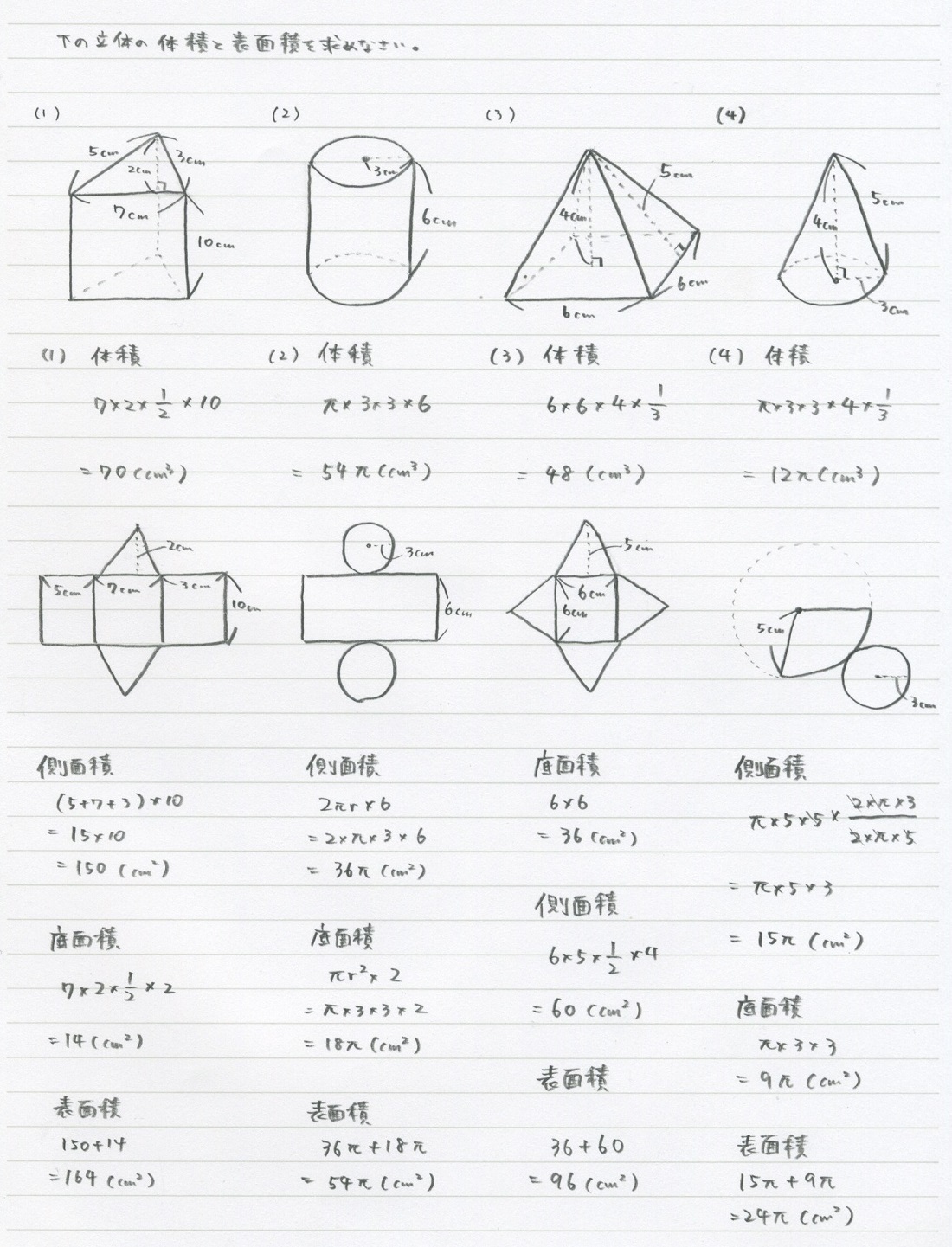



14 2 空間図形 表面積 勉強できようサイト
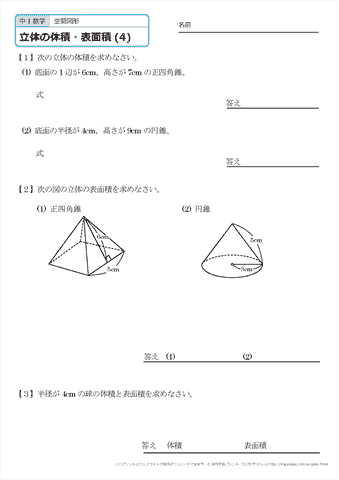



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
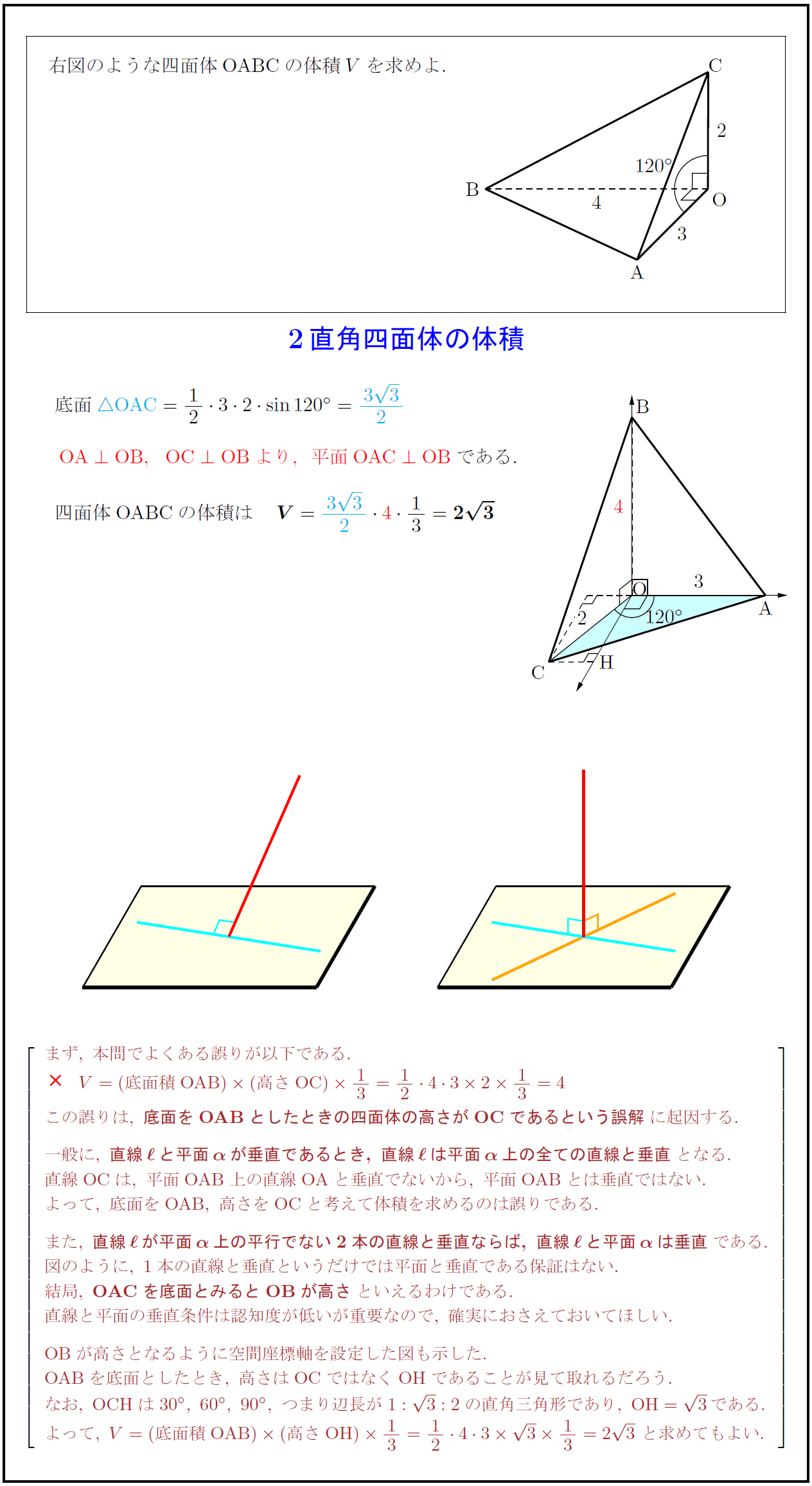



高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月




数学 中3 69 三平方 空間図形への利用 円錐編 Youtube



0 件のコメント:
コメントを投稿