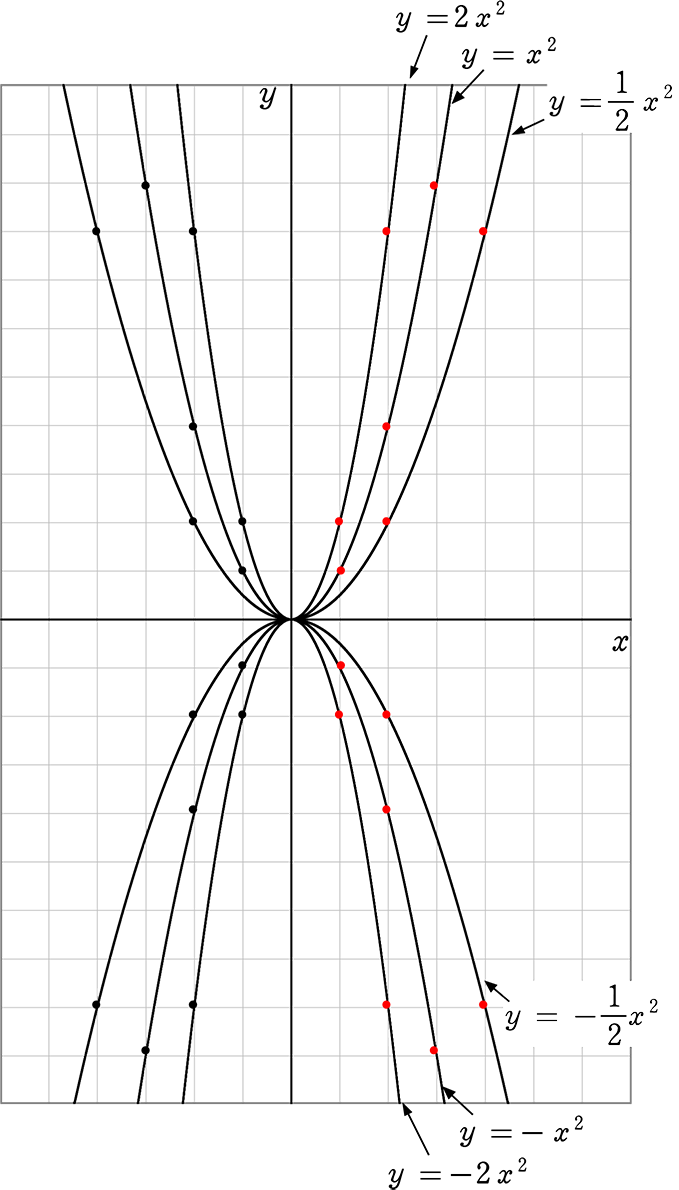
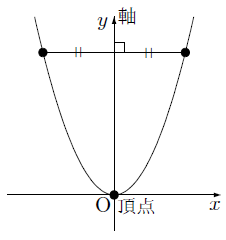
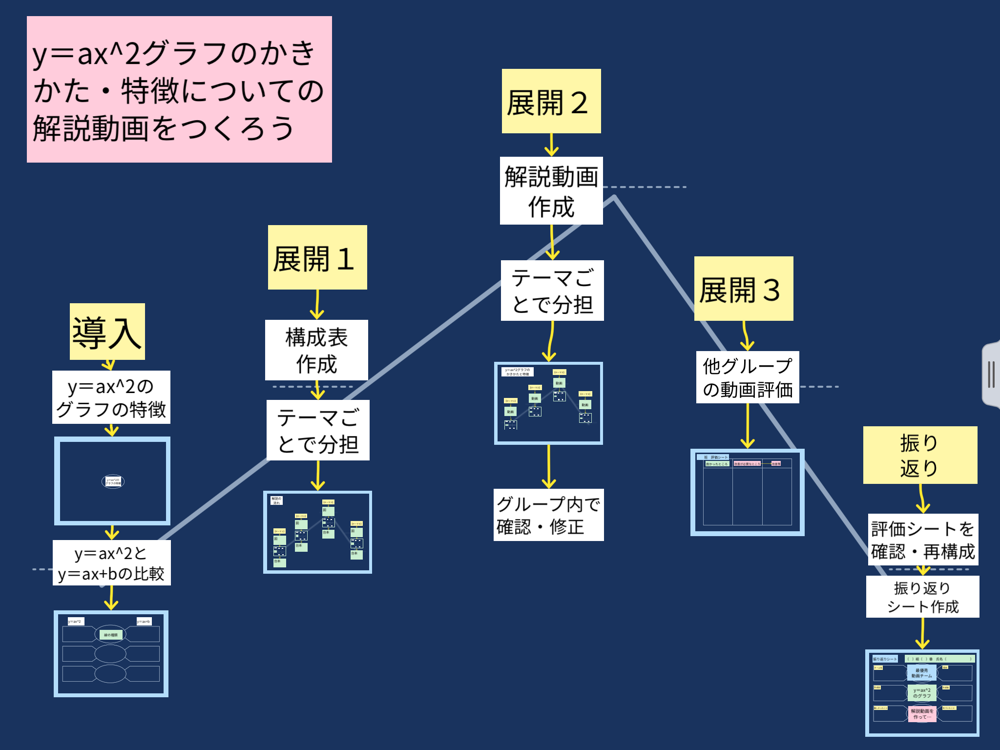
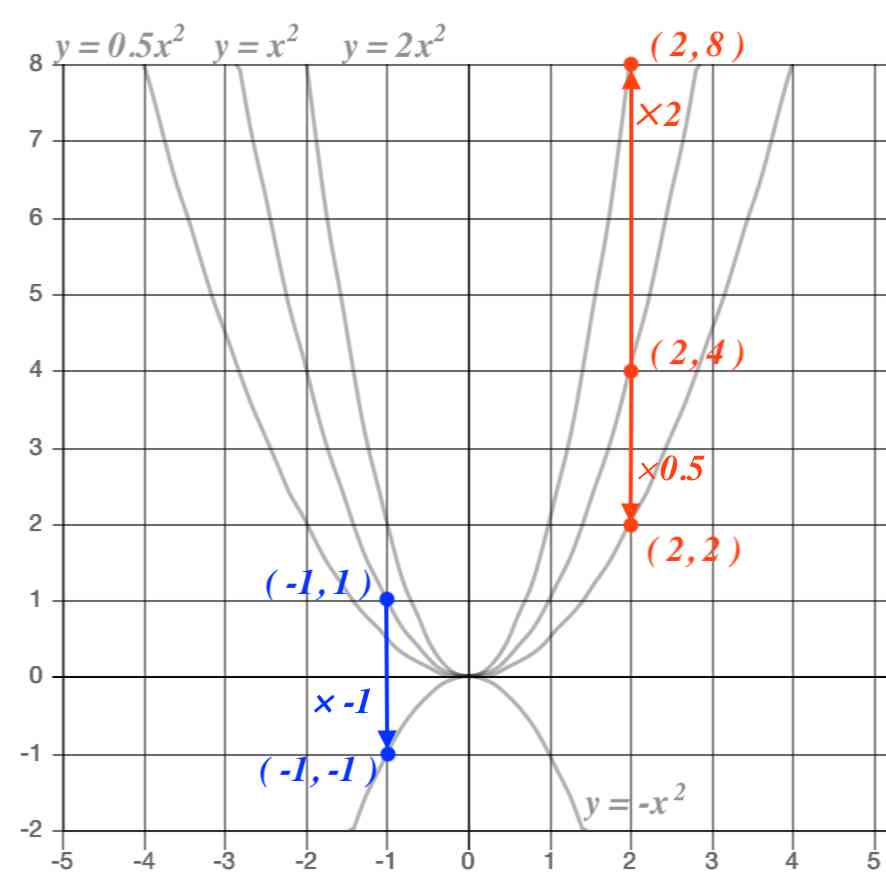
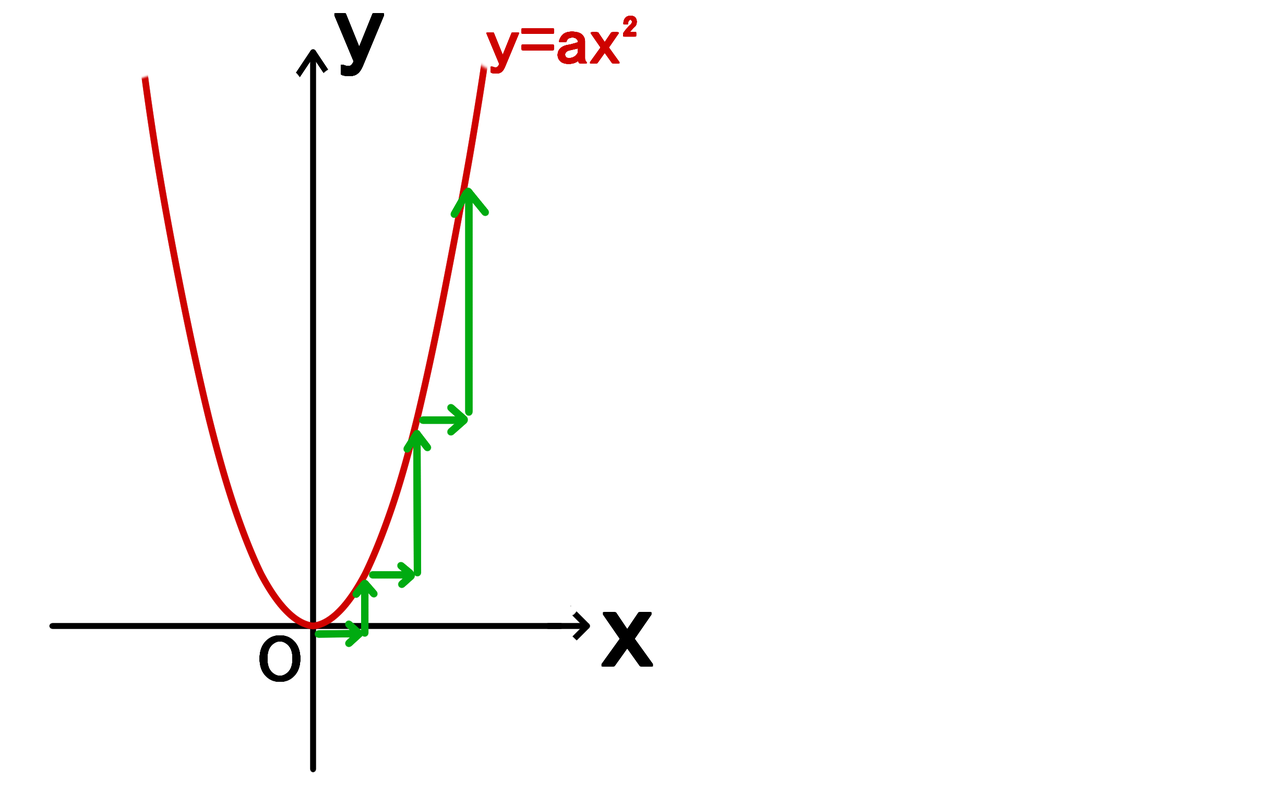
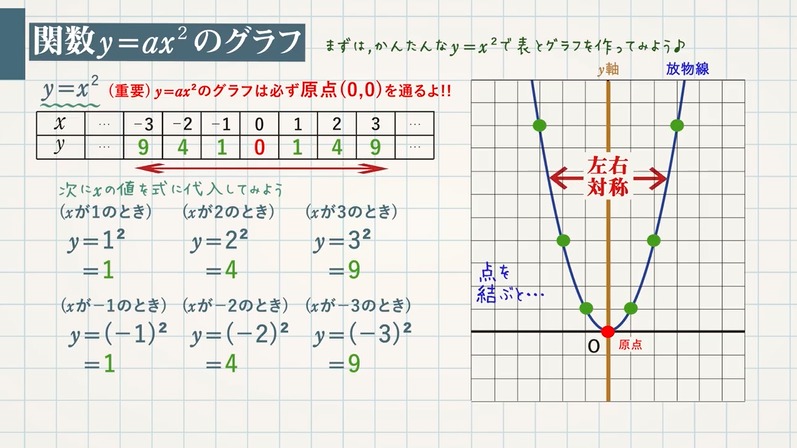
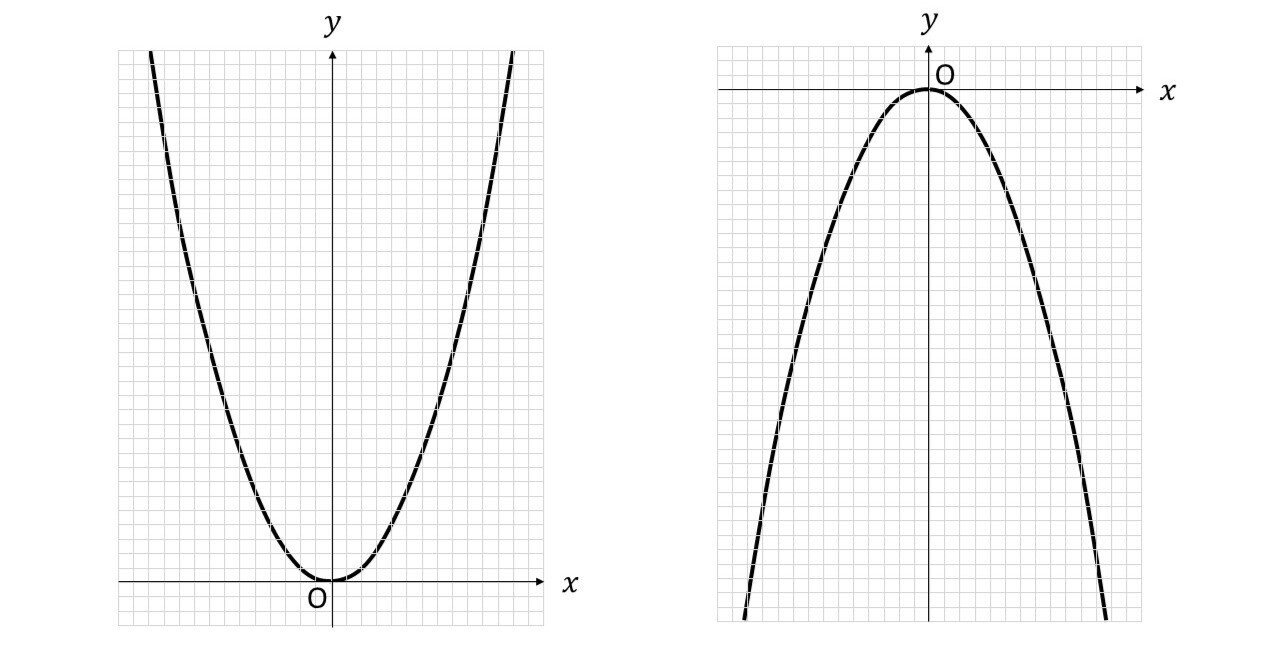
Webx x の変域をすべての数としてグラフにすると, y =x2 y = x 2 のグラフは原点を通り y y 軸について対称な放物線です。 実施時期 3年生2学期(9月) 単元項目 4章1節 関数 y=ax2 y =
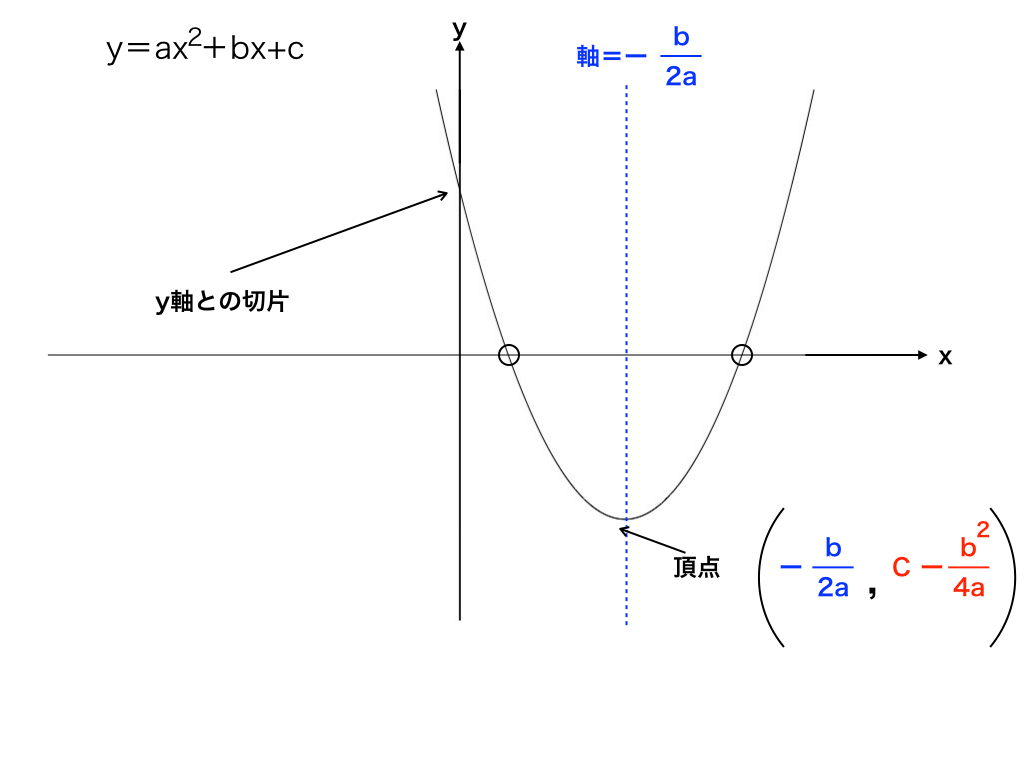
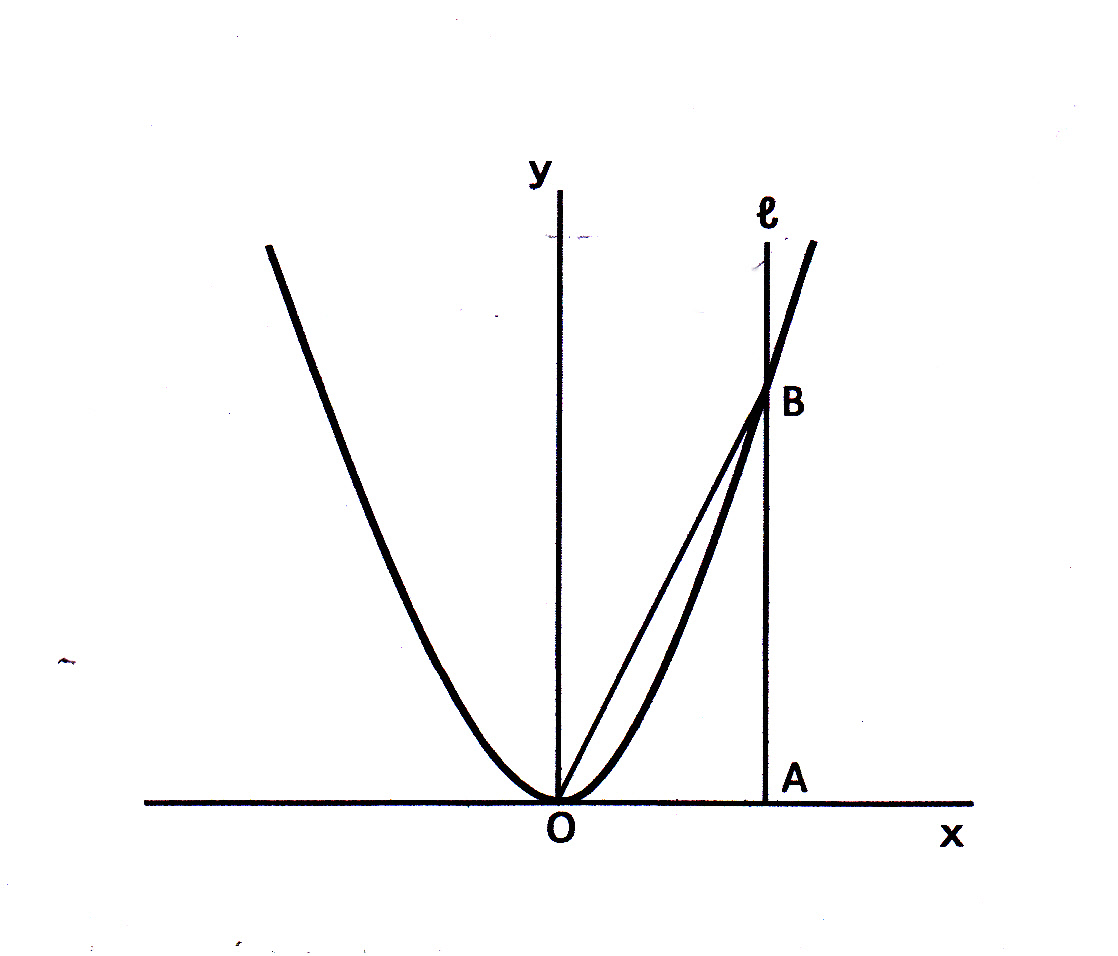
Y=ax2 グラフ 書き方-Web右図のように2次関数 y=x 2 のグラフと直線 y=x2 のグラフが x 軸, y 軸と交わる点をそれぞれ D , C とするとき,次の問いに答えなさい. (1) 点 C , D の座標を求めなさい. (2) 点 PWebこれは暗記するようなものではなく、毎回計算して導き出すものである。 ここまで見たように、2次関数 y = f ( x) = a x 2 b x c のグラフは放物線になる。 そこで、「2次関数 y = a x
Y=ax2 グラフ 書き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 | 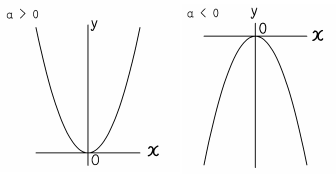 | |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 | ||
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 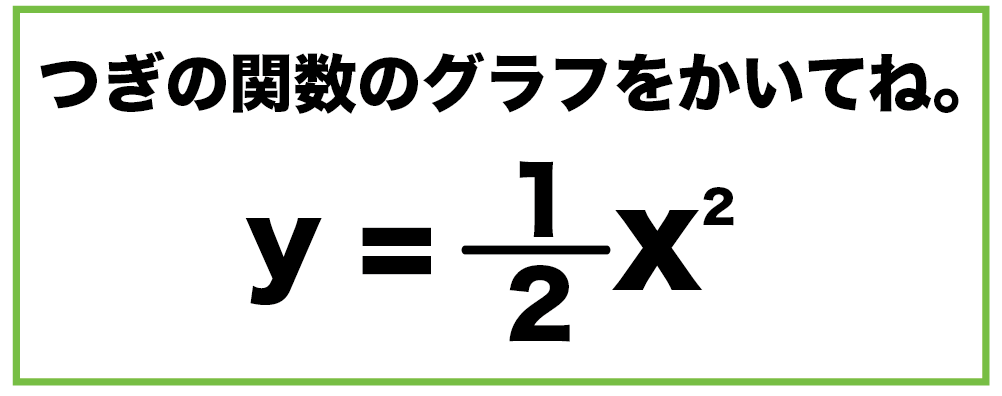 |  |
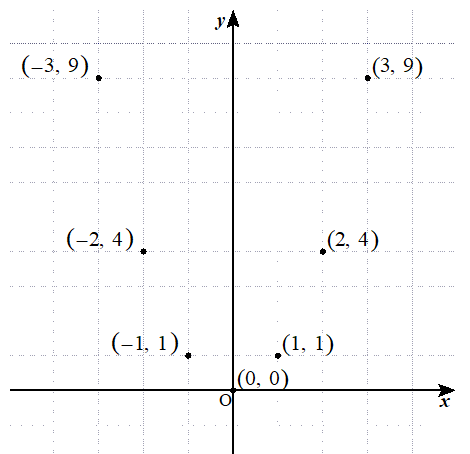 |  |  |
 |  | |
 |  |  |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「Y=ax2 グラフ 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
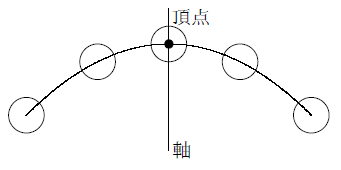
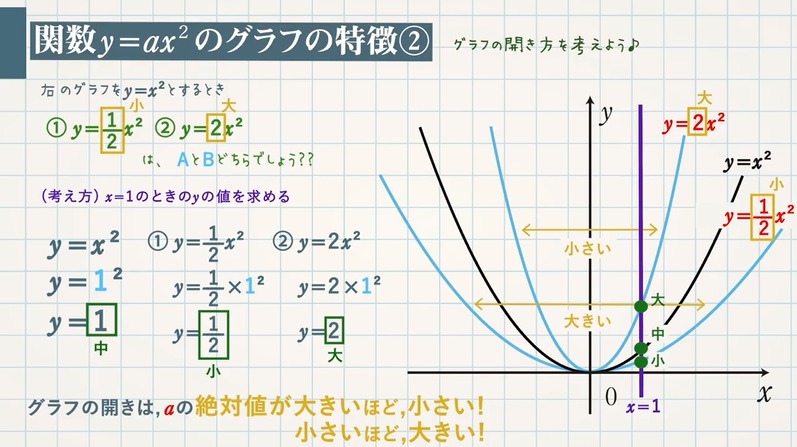
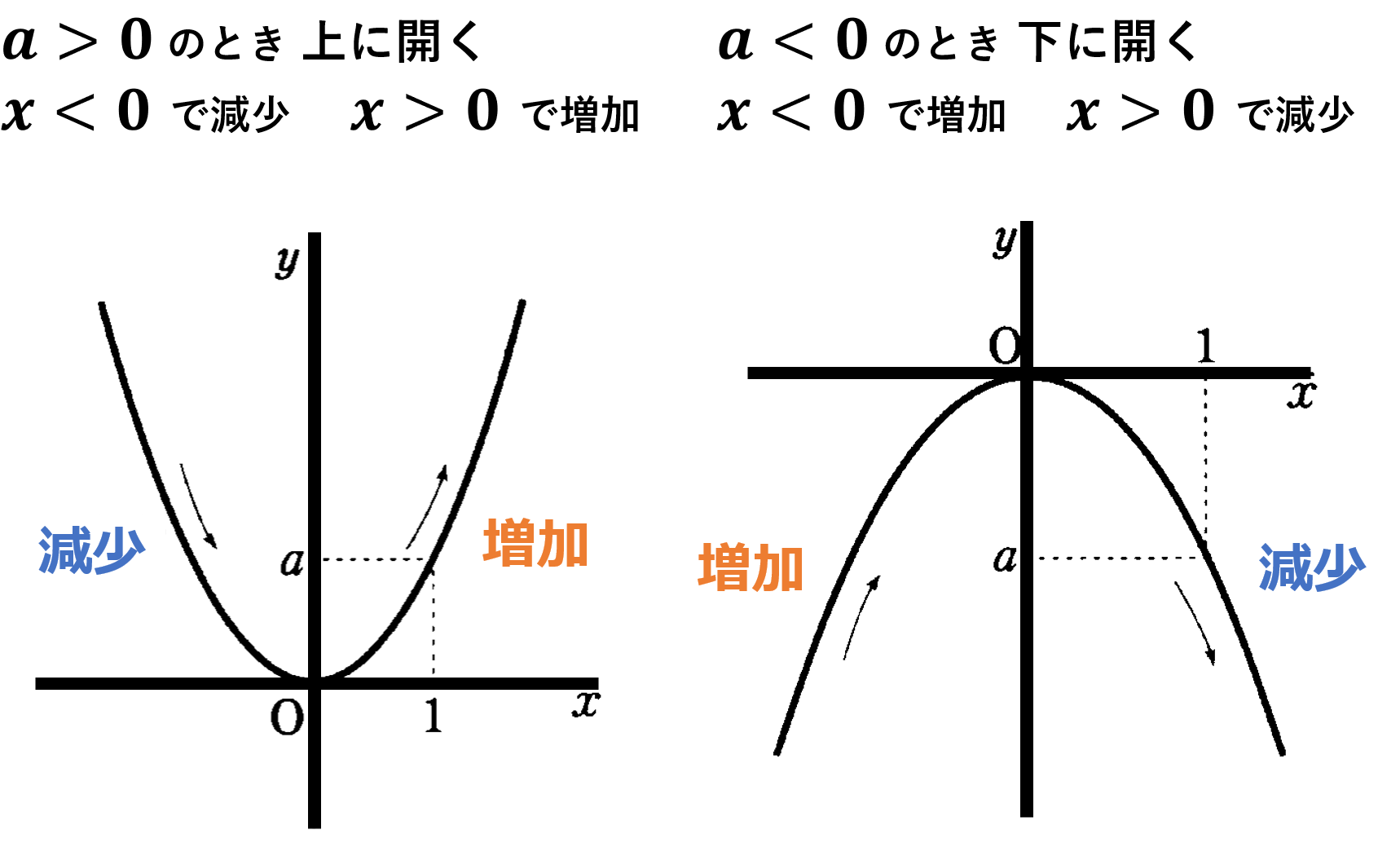
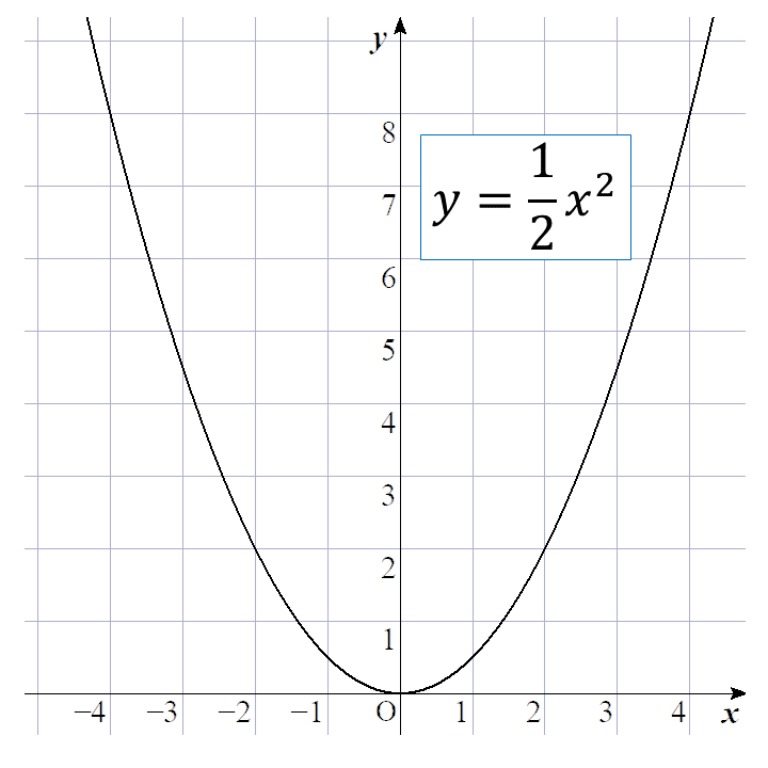
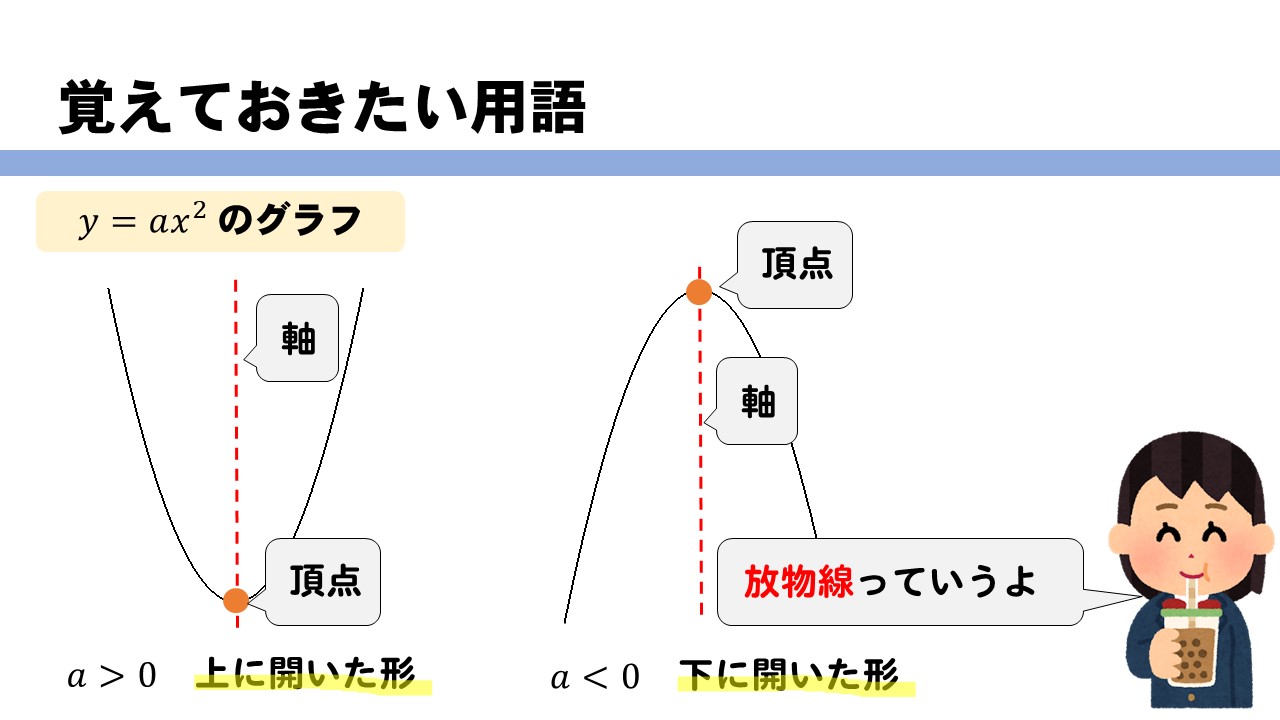
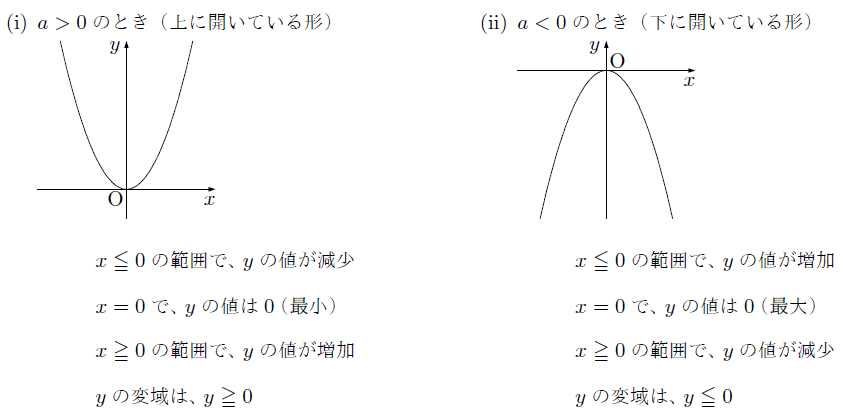
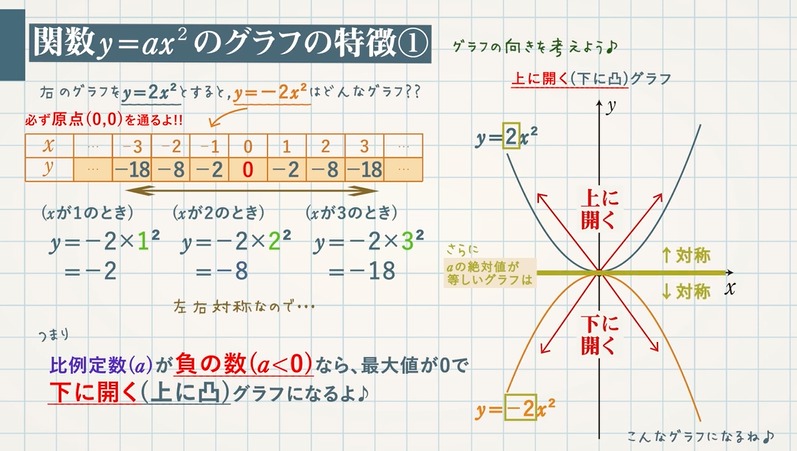
Web原点を通る y 軸に対称 y=ax^2のグラフの形を「放物線」という 放物線の尖がっている先っちょを「頂点」という 原点が頂点になる y=ax^2 の a が正のとき、放物線は上に開く(下にWeb関数y=ax2乗のグラフの特徴\(3\) \(a\)がプラスのときは、上に開いた形になります。 例えば、\(y=\frac{1}{2}x^2\)のグラフは上に開いた形になります。 \(3\)、\(a\)がプラスのときは、上
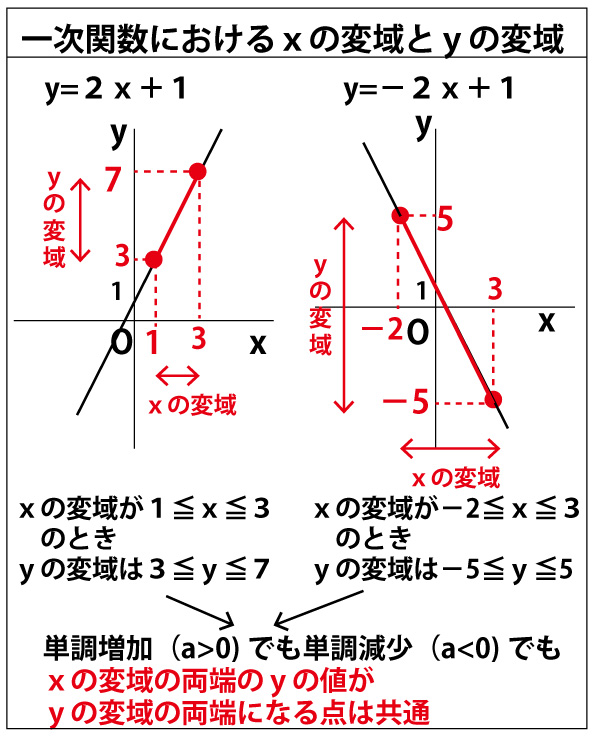
Incoming Term: y=ax2 グラフ, y=ax2 グラフ 特徴, y=ax2 グラフ 問題, y=ax2 グラフ 書き方, y=ax2 グラフ 面積, y=ax2 グラフ aの求め方, y=ax2 グラフ 変域, y=ax2 グラフ 頂点, y=ax2 グラフ用紙, y=ax2 グラフの特徴,




0 件のコメント:
コメントを投稿